| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 2493 백준
- 백준 1464
- 결정 문제
- 뒤집기 3
- 깊이 우선 탐색
- 1939백준
- 재귀
- 그래프이론
- 분할정복
- 그래프 이론
- 구현
- DP
- 브루트포스
- 이분탐색
- 그래프탐색
- 최장길이바이토닉수열
- boj 1464
- 패스트캠퍼스
- 그래프 탐색
- 결정문제
- 비트마스킹
- 최장증가수열
- 서로소 집합
- Lis
- disjoint set
- parametric search
- 백준 뒤집기 3
- union find
- bfs
- 이분 탐색
- Today
- Total
알고리즘 문제풀이
서로소 집합 ( Disjoint Set Unit ) 자료구조 본문
서로소 집합 ( Disjoint Set Unit, DSU ) 이란 ?
공통 원소가 없는 상호베타적인 부분 집합들로 나눠 진 원소들에 대한 정보를 저장하고 조작하는 자료구조.
DSU는 해당 원소가 같은 집합 내에 포함되어 있는지 빠르게 확인하기 위해서 사용되는 자료구조이다.
공통 원소를 포함하고 있지 않는 집합이므로, 교집합 or 차집합 등의 연산은 불필요하다.(= 의미가 없다)
핵심 연산( Union - Find )
-
Union 연산 : 2개의 DSU를 하나의 Set으로 합쳐주는 연산
-
Find 연산 : 어떤 element 가 주어 질 때, 이 Element가 속해있는 집합의 대표원소를 반환
*대표 원소가 같다 -> 같은 서로소 집합 에 속해 있다는 것.
Disjoint Set은 Array, Linked List, Tree 등으로 구현 할 수 있는데
이 중 Tree로 구현하는 것이 성능면에서 월등히 우수하다. ( 비교 내용은 더보기를 참고하자 )
1. Array 방식 : disjointSet[i] 가 i번째 노드의 대표원소를 저장한다고 생각하자.
서로소 집합을 Array로 구현 할 경우, Find연산은 배열에 직접 접근하여 값을 가져오는 만큼 O(1)의 시간복잡도를 가질 것이다. 반면에 Union 연산은 어떨까? 서로소 집합 A 를 서로소 집합 B에 Union하고 싶다. 이럴 경우 A에 있는 모든 원소들을 순차적으로 탐색하며, 서로소 집합 B의 대표원소의 값으로 변경해주어야 하므로 O(N)의 시간복잡도를 가질 것이다.
2. Linked List 방식 : 각 서로소 집합을 Linked List로 구현한다고 생각하고 해당 Linked List의 Head부분에 해당 집합의 대표 원소를 저장한다고 생각하자.
연결 리스트 내부의 각 노드마다 헤드로 직접 접근할 수 있는 포인터를 가지고 있을 경우에도 Find연산에는 O(1)의 시간이 소요되고
Union연산시에는 덧붙여 지는 각 원소들이 새로운 리스트의 헤드를 가리킬 수 있도록 값을 갱신해야하기 때문에 이 또한, O(N)의 시간이 소요된다.3. Tree 방식 ( Disjoint Set Forest ): 서로소 집합을 Tree로 구현할 때, Tree 의 루트 노드를 해당 서로소 집합의 대표원소 라고 생각하자.
Find 연산
트리 방식으로 구현 할 경우 트리 내부(즉, 서로소 집합에 포함 된)의 원소의 대표 값을 알기 위해서 자신의 부모 노드 부터 ~ 루트 노드 까지 순차적으로 접근하며 루트 노드에 도달 할 경우 해당 노드의 값을 리턴하는 방식으로 구현 할 수 있겠다.
이 경우, 시간복잡도는 Tree의 Depth에 비례할 것이다.
Union 연산
간단하다!
서로소 집합을 표현한 A,B 라는 트리가 있다고 가정하자, A 에서 B로 Union 을 시키고 싶다.
A라는 트리의 루트 노드가 A라는 서로소 집합을 표현하므로 A의 루트 노드의 부모노드로 B의 루트 노드를 가리키도록 구현 하면
시간복잡도는 O(1)이 된다.
우리는 Tree를 이용하여 Disjoint Set 을 구현할 것이다.
트리로 구현 할 경우 해당 서로소 집합을 표현하는 대표원소는 해당 트리의 루트 노드가 된다.
자식 노드에서 Find를 통해서 대표원소(=루트 노드)에 접근 할 수 있게 하기 위해, 부모노드의 포인터나 인덱스를 저장하고 있어야 한다.
1. 연결 리스트의 형태로 트리를 구현 할 경우 - 루트 노드의 부모는 null 값을 가져야 할 것이다.
2. 배열의 형태로 트리를 구현 할 경우 - 루트 노드의 부모는 자기 자신의 인덱스를 가져야 할 것이다.
우리는 2번째 방식을 이용하여 트리를 구현 할 예정이다. ( 배열이 코드 상으로 좀 더 깔끔하다.. )
직관적인 구현 ( Disjoint Set Forest )
struct FirstDisjointSet{
vector<int> parent; // 부모의 인덱스를 나타낸다.
// 초기에 상태에서 자기 자신을 대표원소로 가진다.
FirstDisjointSet(int size){
parent.resize(size);
for(int i=0; i<size; i++){
parent[i] = i;
}
}
// Find 연산
int find(int u){
// 루트 노드 일 경우
if( u == parent[u] )
return u;
return find(parent[u]);
}
// union 연산
bool _union(int u, int v){
// u, v의 대표 원소를 찾는다.
u = find(u), v = find(v);
// u와 v가 같은 집합 내에 속해 있다면, union 할 필요가 없다.
if( u == v ) return false;
parent[u] = v;
return true;
}
};맨 처음, DisjointSet이 생성될 때 기본적으로 모든 원소들은 독립적인 집합들로 이루어 진다. 이 때, 대표원소는 자기 자신이므로 parent 를 자기 자신과 동일하게 초기화 시킨다.
1. Find
재귀 함수를 이용하여 부모 노드들을 경유하며, 루트 노드 까지 다다를 수 있게 구현 하였다.
base 조건은 대표원소의 특징인 parent == u(자기 자신) 으로 설정 해 주었다.
2. Union
하나의 원소가 속해 있는 서로소 집합의 대표원소를 구한 후 나머지 원소의 대표원소를 구한다.
대표 원소가 같은 경우, 2개의 원소가 같은 서로소 집합에 속해 있다는 의미이므로 Union이 실패했음을 알리고 (false 리턴) 종료한다.
그렇지 않은 경우, 하나의 대표 원소(u)의 부모를 v로 설정해 주면서 종료한다. (-> 이 경우 u 를 v 에 포함 시키는 것이 된다.)
최악의 경우?
위와 같은 방식으로 구현 할 경우, 합쳐진 새로운 서로소 집합 C가 높이가 계속 높아져 최악의 경우 한 쪽으로 치우친 unbalanced 한 트리의 형태를 가지게 된다.

이럴 경우, 연결 리스트와 다름이 없는 상태로 find 연산시에 루트노드에 접근하기 위해 O(N)이라는 시간이 소요된다.
이러한 상황을 피하고자 Union By Rank를 이용한 최적화를 사용할 수 있다.
1. Union By Rank
트리에서 대표원소를 찾기 위해 부모노드 ~ 루트노드 까지의 경로를 순차적으로 방문하는 것을 알 수있다.
즉, Find함수는 트리의 depth와 비례한다.
그러면 트리의 depth를 최대한 적게 유지할 수 있을까?
결론 부터 말하자면 있다!
Union간의 기준을 부여하면 된다. 일반적으로 높이가 낮은 트리를 높이가 높은 트리밑에 합병하면서 트리의 높이가 높아지는 것을 어느정도 경감시킬 수 있다. 이것을 Union by Rank 라고 한다.
예시



첫번 째 트리는 Union 시 발생할 수 있는 최악의 상황이라고 할 수 있다. 높이가 높은 트리를 높이가 낮은 트리 밑에 포함 시키므로서, 합병한 전체 그래프의 높이를 증가 시켰다는 것을 알 수 있다.
두번 째 트리는 Union By rank 를 이용하여 높이가 낮은 트리를 높이가 높은 트리 아래로 포함 시키므로서, 전체 그래프의 높이는 높이가 높은 트리의 높이와 같다는 것을 알 수 있다.
( 높이가 같은 경우에만, 합병한 트리의 높이가 높아진다. )
Union by Rank 를 위해, 원래 코드에서 Union 연산을 다음과 같이 수정해 준다.
// union 연산
bool _union(int u, int v){
// u, v의 대표 원소를 찾는다.
u = find(u), v = find(v);
// u와 v가 같은 집합 내에 속해 있다면, union 할 필요가 없다.
if( u == v ) return false;
// Union By Rank ( 높이가 높은 트리 아래에 높이가 낮은 트리를 병합 ) -> 병합 된 트리의 높이 변화 없음
if( rank[u] > rank[v] )
parent[v] = u;
else if( rank[u] < rank[v] )
parent[u] = v;
// 높이가 같을 때
else{
parent[u] = v;
rank[v] += 1;
}
return true;
}
2. path compression (경로 압축)
Union By rank 를 통한 트리의 높이에 대한 최적화를 끝냈음에도 불구하고 신경 쓰이는 점이 하나 더 있을 것이다.
굳이 find 함수를 호출 할 때 마다 순차적으로 루트노드에 접근하여 값을 가져오는 것을 반복해야할까?
Find 함수를 수행하면서 루트노드를 발견하면 그 값을 저장하여, 하위의 모든 자식의 경로를 루트노드를 바로 가리키게 만들 면 되지 않을까?
Find 함수 수행 마다, 경로를 압축 시켜 주기 위하여 재귀적으로 탐색하되 대표원소를 찾으면 그 값을 리턴해주는 식으로 순차적으로 Find하고자 하는 원소와 루트 노드 사이의 모든 노드들의 경로를 압축 시켜준다.
그렇게 되면, 다음에 Find를 통해 대표원소에 접근할 때에는 O(1)의 시간으로도 접근이 가능할 것이다.
소스코드는 다음과 같다.
// Find 연산
int find(int u){
// 루트 노드 일 경우
if( u == parent[u] )
return u;
// 루트 노드를 찾을 경우 top-bottom 으로 재귀적으로 return 되면서 부모를 루트노드로 초기화 시켜준다.
return parent[u] = find(parent[u]);
}
경로 압축이 수행 되는 과정을 살펴 보자.


Find(1)을 호출해주면, 처음에는 루트 노드 까지 순차적으로 접근하는데, 루트 노드를 찾고 난 다음 해당 루트 노드의 대표원소 값으로 루트 ~ 원소 사이의 모든 노드들의 부모를 수정해주므로서, 다음에 find(1)을 호출 할 시에 순차적으로 탐색하지 않고 바로 접근 할 수 있게 만들어 준다.
모든 노드들이 경로 압축을 마치고 난 후 트리는 다음과 같다.
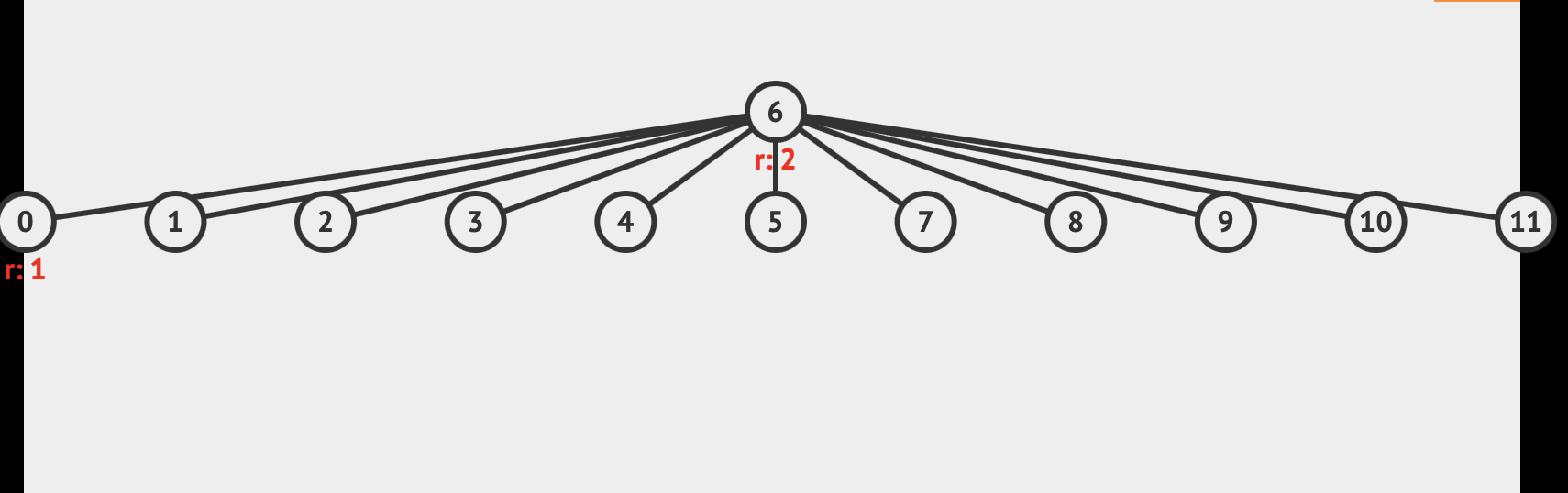
2가지 최적화 기법을 모두 적용한 소스 코드는 다음과 같다.
struct ImprovedDisjointSet{
vector<int> parent; // 부모의 인덱스를 나타낸다.
vector<int> rank;
// 초기에 상태에서 자기 자신을 대표원소로 가진다.
ImprovedDisjointSet(int size){
parent.resize(size);
rank.resize(size,1); // 초기 상태의 높이(rank)는 1이다.
for(int i=0; i<size; i++){
parent[i] = i;
}
}
// Find 연산
int find(int u){
// 루트 노드 일 경우
if( u == parent[u] )
return u;
// 루트 노드를 찾을 경우 top-bottom 으로 재귀적으로 return 되면서 부모를 루트노드로 초기화 시켜준다.
return parent[u] = find(parent[u]);
}
// union 연산
bool _union(int u, int v){
// u, v의 대표 원소를 찾는다.
u = find(u), v = find(v);
// u와 v가 같은 집합 내에 속해 있다면, union 할 필요가 없다.
if( u == v ) return false;
// Union By Rank ( 높이가 높은 트리 아래에 높이가 낮은 트리를 병합 ) -> 병합 된 트리의 높이 변화 없음
if( rank[u] > rank[v] )
parent[v] = u;
else if( rank[u] < rank[v] )
parent[u] = v;
// 높이가 같을 때
else{
parent[u] = v;
rank[v] += 1;
}
return true;
}
};'자료구조 + 알고리즘 > 기초' 카테고리의 다른 글
| 최소 공통 조상(Lowest Common Ancestor, LCA) 알고리즘 (0) | 2021.08.16 |
|---|---|
| Trie(트라이) 자료구조 (0) | 2021.08.10 |
| Manacher 알고리즘 (0) | 2021.05.21 |
| CCW(Counter-Clockwise) 알고리즘 (0) | 2021.02.06 |
| 삽입정렬( Insertion sort ) (0) | 2020.11.11 |




