| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- union find
- parametric search
- 이분 탐색
- 최장길이바이토닉수열
- DP
- 1939백준
- 그래프이론
- 패스트캠퍼스
- boj 1464
- 깊이 우선 탐색
- 이분탐색
- 결정 문제
- 분할정복
- 결정문제
- 비트마스킹
- 최장증가수열
- 브루트포스
- Lis
- 백준 1464
- 뒤집기 3
- 구현
- 그래프 탐색
- 그래프탐색
- 서로소 집합
- disjoint set
- bfs
- 재귀
- 그래프 이론
- 2493 백준
- 백준 뒤집기 3
- Today
- Total
알고리즘 문제풀이
[BOJ] 3015번 - 오아시스 재결합 본문
백준 3015번 - 오아시스 재결합
| 시간제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 256 MB | 7690 | 1864 | 1333 | 24.925% |
문제
오아시스의 재결합 공연에 N명이 한 줄로 서서 기다리고 있다.
이 역사적인 순간을 맞이하기 위해 줄에서서 기다리고 있던 백준이는 갑자기 자기가 볼 수 있는 사람의 수가 궁금해 졌다.
두 사람 A와 B가 서로 볼 수 있으려면, 두 사람 사이에 A 또는 B보다 키가 큰 사람이 없어야 한다.
줄에 서있는 사람의 키가 주어졌을 때, 서로 볼 수 있는 쌍의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 줄에서 기다리고 있는 사람의 수 N이 주어진다. (1 ≤ N ≤ 500,000)
둘째 줄부터 N개의 줄에는 각 사람의 키가 나노미터 단위로 주어진다. 모든 사람의 키는 231 나노미터 보다 작다.
사람들이 서 있는 순서대로 입력이 주어진다.
출력
서로 볼 수 있는 쌍의 수를 출력한다.
예제 입력 1
7
2
4
1
2
2
5
1예제 출력 1
10출처
https://www.acmicpc.net/problem/3015
3015번: 오아시스 재결합
첫째 줄에 줄에서 기다리고 있는 사람의 수 N이 주어진다. (1 ≤ N ≤ 500,000) 둘째 줄부터 N개의 줄에는 각 사람의 키가 나노미터 단위로 주어진다. 모든 사람의 키는 231 나노미터 보다 작다. 사람
www.acmicpc.net
알고리즘 분류
- 자료구조
- 스택
접근 방법
먼저, 한 줄에 한명 씩 들어오면서 짝이 지어지는 경우를 더한다고 생각해보자.
새로 들어오는 사람(${A_j}$) 와 짝이 지어지는 경우는 ${A_i > A_j }$ (i<j) 를 만족하는 i의 최댓값에 대해 (i~j)까지의 영역일 것이다.
말로 하면 이해하기 어려우니, 그림으로 살펴보자.

A영역은 새로 들어오는 사람이 볼 수 없는 사람들이므로 이 부분까지 탐색 할 이유가 없다.
고로, 우리는 B영역만 탐색을 진행하면 된다. ${A_i}$의 정의에 따라, B영역의 모든 원소는 ${A_j}$보다 작거나 같다.
B영역에 속하는 원소의 개수를 정답에 더한 다음, 새로운 사람(${A_k}$)이 더 들어오는 상황을 생각하자.
이전 단계에서 B를 B'으로 표현하였다.
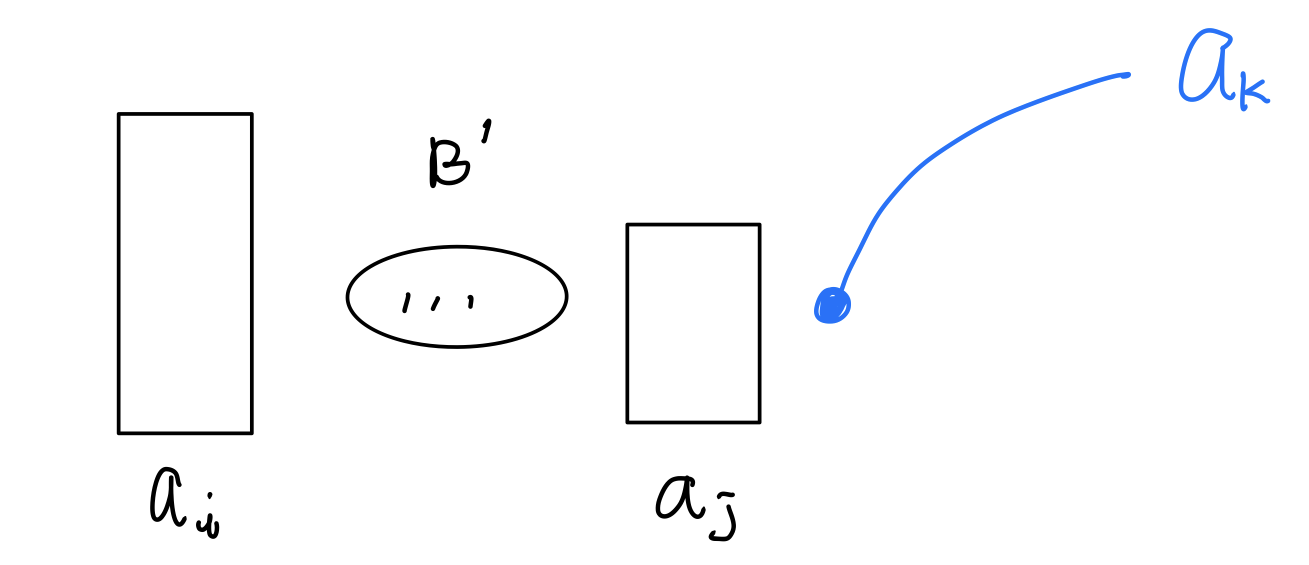
그렇다면, 여기서 케이스를 구분해줄 수 있다.
Case1. ${A_k < A_j}$ 경우
-> 이 때, ${A_k}$는 ${A_j}$ 만 짝을 지어줄 수 있고 이전의 B'영역은 탐색하지 않는다.
Case2. ${A_k == A_j}$ 경우
-> 이 때, ${A_k}$는 ${A_j}$와 이전의 B'영역들과 짝을 지어 줄 수 있다.
Case3. ${A_k > A_j}$ 경우
-> 이전 스테이지에서 했던 것 처럼 ${A_k}$보다 큰 ${A_l}$중 l의 최댓값을 찾아서 (l~k)까지의 원소들을 더해준다.
(이전 단계에서, B영역을 구하는 것과 동일함)

새로운 탐색 영역(B)도 A_k보다는 작거나 같은 원소들로 구성된다.
자 그러면, 규칙을 찾았다.
${A_l}$과 새로운 영역 B를 포괄하는 부분을 stack으로 관리해주자.
그러면 stack은 항상 내림차순을 유지하게 될 것이다.
이 후, 탐색에서도 새롭게 추가되는 ${A_{new}}$에 대해 ${A_m}$이 ${A_{new}}$ 보다 큰 최대의 m을 찾을 때 까지 스택의 원소를 pop하면서 개수를 정답에 추가한다.
여기서, 예외가 존재한다. 바로, 스택의 원소들 중 ${A_{new}}$와 값이 동일할 때이다. 이 때 스택에서 pop을 한다면 다음 스테이지에서 들어오는 사람에 대해서 해당 스택의 원소는 고려되지 못한다.
이 같은 경우, 스택에 존재하는 동일한 원소의 개수를 또 다른 값으로 저장하여 추가해주는 방식으로 해결할 수 있다.
소스 코드
#include <bits/stdc++.h>
using namespace std;
int main(void){
ios_base::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
long long N, ans = 0;
cin >> N;
stack<pair<int,int>> stk;
for(int i=0; i<N; i++){
int h, cnt = 1;
cin >> h;
while( !stk.empty() && stk.top().first <= h ){
if( stk.top().first == h ){
ans += stk.top().second;
cnt = stk.top().second + 1;
stk.pop();
}else{
ans += stk.top().second;
cnt = 1;
stk.pop();
}
}
if( !stk.empty() ) ans += 1;
stk.push({h, cnt});
}
cout << ans ;
return 0;
}
'자료구조 + 알고리즘 > [BOJ]' 카테고리의 다른 글
| [BOJ] 10749번 - Superbull (0) | 2021.12.30 |
|---|---|
| [BOJ] 13334번 - 철로 (0) | 2021.08.30 |
| [BOJ] 5719번 - 거의 최단 경로 (0) | 2021.08.15 |
| [BOJ] 2696번 - 중앙값 구하기 (0) | 2021.08.14 |
| [BOJ] 14725번 - 개미굴 (0) | 2021.08.11 |


