| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 패스트캠퍼스
- DP
- 그래프탐색
- Lis
- 재귀
- 뒤집기 3
- disjoint set
- 분할정복
- 그래프이론
- 최장길이바이토닉수열
- 최장증가수열
- 이분탐색
- 깊이 우선 탐색
- 결정 문제
- 구현
- 그래프 이론
- 브루트포스
- bfs
- union find
- 백준 1464
- 그래프 탐색
- 이분 탐색
- 1939백준
- 결정문제
- 2493 백준
- parametric search
- 비트마스킹
- 서로소 집합
- 백준 뒤집기 3
- boj 1464
- Today
- Total
알고리즘 문제풀이
[BOJ] 11657 번 - 타임머신 본문
백준 11657번 - 타임머신
| 시간제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 256 MB | 24640 | 2472 | 1534 | 16.807% |
문제
N개의 도시가 있다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 버스가 M개 있다. 각 버스는 A, B, C로 나타낼 수 있는데, A는 시작도시, B는 도착도시, C는 버스를 타고 이동하는데 걸리는 시간이다. 시간 C가 양수가 아닌 경우가 있다. C = 0인 경우는 순간 이동을 하는 경우, C < 0인 경우는 타임머신으로 시간을 되돌아가는 경우이다.
1번 도시에서 출발해서 나머지 도시로 가는 가장 빠른 시간을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.
출력
만약 1번 도시에서 출발해 어떤 도시로 가는 과정에서 시간을 무한히 오래 전으로 되돌릴 수 있다면 첫째 줄에 -1을 출력한다. 그렇지 않다면 N-1개 줄에 걸쳐 각 줄에 1번 도시에서 출발해 2번 도시, 3번 도시, ..., N번 도시로 가는 가장 빠른 시간을 순서대로 출력한다. 만약 해당 도시로 가는 경로가 없다면 대신 -1을 출력한다.
예제 입력 1
3 4
1 2 4
1 3 3
2 3 -1
3 1 -2예제 출력 1
4
3
예제 입력 2
3 4
1 2 4
1 3 3
2 3 -4
3 1 -2예제 출력 2
-1
출처
www.acmicpc.net/problem/11657
11657번: 타임머신
첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.
www.acmicpc.net
알고리즘 분류
- 그래프 이론
- 벨만포드
접근 방법
1번 도시에서 부터 N번 도시 까지 도착할 수 있는 최소 시간을 구하라고 하였으므로
각 도시를 그래프의 정점으로 표현하고 버스 노선의 정보를 간선으로 표현하면 그래프의 형태로 표현이 가능하다는 것을 알 수 있다.
또한, 버스 노선의 정보 중 A->B로 가는데 걸리는 시간이 음수 값이 될 수 있으므로 이 부분을 유의해야한다.
1번 도시에서 부터 K번 도시(K<=N) 까지 도착하는 데 걸리는 최소 시간을 구하는 것이 핵심인데 간선의 Cost 값이 음수가 될 수 있다는 점에서 다익스트라 알고리즘으로 접근하기에는 적절하지 못하다.
또한 문제 조건에서 '1번 도시에서 출발해 어떤 도시로 가는 과정에서 시간을 무한히 오래 전으로 되돌릴 수 있다면 첫째 줄에 -1을 출력한다' 라는 조건이 존재 하므로, 1 번 도시에서 k번 도시 까지 도착하기 까지 음의 사이클의 유/무 도 파악 해주어야 한다.
필자는 벨만 포드 알고리즘을 이용하여 문제를 해결하였다.
첫 번째 실수
처음에 주어 진 간선의 개수 M은 최대 6000개이다.
그에 비해 정점의 개수 N은 최대 500개 이다. 즉, 비둘기 집의 원리에 따라 A->B로 가는 정점이 여러 개 존재 할 수도 있다는 얘기이다.
처음에 인접 행렬로 연결 관계를 표현 했다가 인접 리스트로 수정 하였다.
두 번째 실수
출력초과가 떴다..
출력 초과의 원인으로 -1 만 출력해야하는데 N-1줄에 걸쳐 출력을 한 경우 또는 N-1줄에 걸쳐 출력을 해야하는데 -1 만 출력한 경우가 있을 것이라 생각하였다.
N-1줄에 걸쳐 출력을 해야하는데 -1만 출력하는 경우는 어떤 경우가 있을까?
바로 1번 도시에서 N번 도시 까지 가는 경로에 있어 음의 사이클이 존재하지는 않지만, 전체 그래프 상에서 음의 사이클이 존재했을 때가 이 같은 경우라고 할 수 있다. ( ${1 -> u_1 -> u_2 -> ... -> V}$ 로 가는 경로 중 Negative Cycle이 존재 )
예를 들면, 다음과 같은 경우라고 할 수 있겠다.
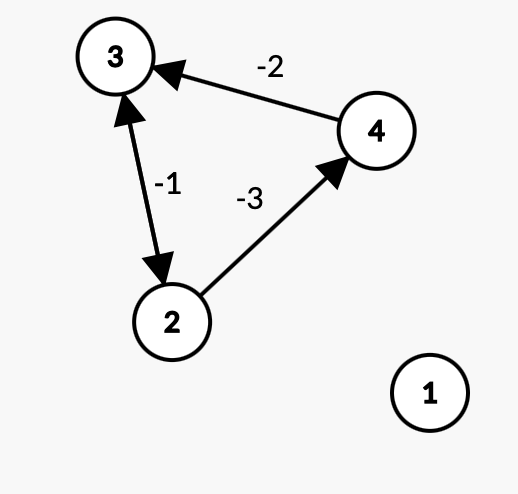
하지만, 경로가 1번 도시에서 K번(K<=N) 도시 까지 도달 할 수 없는 경우에는 dist배열이 갱신이 되질 않으므로 hasNegativeCycle이 변하지도 않았을 것이다. 이 같은 경우는 -1를 N-1개의 줄에 걸쳐 출력하는게 자명하므로 이러한 경우에서 문제가 발생하지는 않았을 것이다.
다음으로 고려해야 할 점은 -1 만 출력해야하는데 N-1줄에 걸쳐 출력하는 경우가 있을 것이다.
이러한 경우는 음의 사이클이 존재 함에도 불구하고 인지하지 못 한 경우가 있을 것이다.
왜 그럴까 생각하던 도중, Int형으로 구현한 dist가 가질 수 있는 최대, 최소 범위를 벗어 날 수도 있는 경우를 발견하였다.
최악의 경우는 500 개의 노드와 6000개의 edge가 모두 -10000의 가중치를 가지게 되는 경우이다.
6000개의 edge가 전부 음의 사이클을 형성한다고 하면, 매 라운드 마다 계속 dist의 값이 줄어들 것이고 음의 사이클을 판별하기 위한 N번째 라운드 이전에 dist가 underflow가 난다( ${500 * 6000 * -10000 \approx -3 * {10}^{10}}$ )
N번 째 라운드가 진행 될 경우에 이미 dist[i]의 값은 INF값 이상의 값이 될 것이고, 이 경우 실제 dist값이 계속 감소하는데도 불구하고 underflow로 인해 dist[next] < dist[i] + cost 인 것으로 판단하여 dist의 값을 갱신하지 않을 것이다.
고로 음의 사이클의 존재가 있음에도 불구하고 없다는 것으로 판단하여 N-1 개의 줄 만큼 출력을 하기 때문에 출력초과 문제가 발생 한 것이다.
위와 같은 문제는 int 형보다 더 큰 범위를 표현할 수 있는 long long 자료형을 사용하면 해결되는 문제이다.
소스 코드
#define INF 1e9
#include <bits/stdc++.h>
using namespace std;
// u -> v 로 가는 edge 가 2개 이상 존재할 수도 있음 ( 비둘기 집의 원리 )
vector<pair<int,int>> adj[501];
vector<long long> dist;
int N, M;
int main(void){
ios_base::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> N >> M ;
for(int i=0; i<M; i++){
int src, dest, cost;
cin >> src >> dest >> cost;
adj[src].push_back({cost, dest});
}
dist.resize(N+1, INF);
dist[1] = 0 ;
bool hasNegativeCycle = false;
for( int round = 1; round <= N ; round ++ ){
// 모든 edge 들을 조사한다.
for(int i=1; i<=N; i++){
for(auto item : adj[i]){
int cost = item.first;
int next = item.second;
if( dist[i] != INF && dist[next] > dist[i] + cost ){
dist[next] = dist[i] + cost;
if( round == N ) hasNegativeCycle = true;
}
}
}
}
// 1 -> v 까지 걸리는 시간을 구하고 싶다. u를 경로 상에 존재하는 또 다른 노드라고 생각하자.
// 1 -> u 로 가는 경로 중 negative cycle 이 있다면
// u -> v 로 가는 경로도 사이클을 따라서 무한히 돌게 된다.
// 문제 조건에 따라, 1 -> v 로 가는 과정에서 무한히 오래 전으로 돌릴 수 있는 경우 -1을 출력하라는 조건이
// 있으므로, 1 -> v 로 가는 길에서 음수 사이클이 존재하는 지 여부를 확인해야하는 것이 맞다.
// 하지만, N번째 라운드에서 hasNegativeCycle이 true 로 바뀌었다는 것은 v로 가는 길이 INF가 아니고
// v로 가는 길이 연결 되어 있고 그 경로 중 음수 사이클이 존재 한다는 것이다.
// 출력 초과의 원인은 바로 데이터형 !
// 최악의 경우 dist[v]의 값은 500 * 6000 * -10000 이 되고 이는 -3 * 10^10 이므로
// int형을 표현 할 경우 underflow 가 남.
if( hasNegativeCycle )
cout << -1 << '\n';
else{
for(int i=2; i<=N; i++){
if( dist[i] >= INF ) cout << -1 << '\n';
else cout << dist[i] << '\n';
}
}
return 0;
}
'자료구조 + 알고리즘 > [BOJ]' 카테고리의 다른 글
| [BOJ] 10429번 - QUENTO (0) | 2020.12.17 |
|---|---|
| [BOJ] 16234번 - 인구 이동 (0) | 2020.12.17 |
| [BOJ] 1976 번 - 여행 가자 (0) | 2020.12.12 |
| [BOJ] 15591 번 - MooTube(Silver) (0) | 2020.12.11 |
| [BOJ] 14503 - 로봇 청소기 (0) | 2020.12.09 |


