| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 분할정복
- parametric search
- 그래프 이론
- 패스트캠퍼스
- 2493 백준
- 서로소 집합
- DP
- bfs
- Lis
- 뒤집기 3
- 브루트포스
- 최장증가수열
- 비트마스킹
- disjoint set
- 구현
- 그래프탐색
- 이분탐색
- 그래프이론
- 1939백준
- 이분 탐색
- 깊이 우선 탐색
- 백준 뒤집기 3
- boj 1464
- 최장길이바이토닉수열
- 그래프 탐색
- union find
- 결정 문제
- 백준 1464
- 결정문제
- 재귀
- Today
- Total
알고리즘 문제풀이
[BOJ] 17070번- 파이프 옮기기 1 본문
백준 17070번 - 파이프 옮기기 1
| 시간제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 512 MB | 10446 | 5132 | 3398 | 49.296% |
문제
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의 번호이고, 행과 열의 번호는 1부터 시작한다. 각각의 칸은 빈 칸이거나 벽이다.
오늘은 집 수리를 위해서 파이프 하나를 옮기려고 한다. 파이프는 아래와 같은 형태이고, 2개의 연속된 칸을 차지하는 크기이다.

파이프는 회전시킬 수 있으며, 아래와 같이 3가지 방향이 가능하다.

파이프는 매우 무겁기 때문에, 유현이는 파이프를 밀어서 이동시키려고 한다. 벽에는 새로운 벽지를 발랐기 때문에, 파이프가 벽을 긁으면 안 된다. 즉, 파이프는 항상 빈 칸만 차지해야 한다.
파이프를 밀 수 있는 방향은 총 3가지가 있으며, →, ↘, ↓ 방향이다. 파이프는 밀면서 회전시킬 수 있다. 회전은 45도만 회전시킬 수 있으며, 미는 방향은 오른쪽, 아래, 또는 오른쪽 아래 대각선 방향이어야 한다.
파이프가 가로로 놓여진 경우에 가능한 이동 방법은 총 2가지, 세로로 놓여진 경우에는 2가지, 대각선 방향으로 놓여진 경우에는 3가지가 있다.
아래 그림은 파이프가 놓여진 방향에 따라서 이동할 수 있는 방법을 모두 나타낸 것이고, 꼭 빈 칸이어야 하는 곳은 색으로 표시되어져 있다.
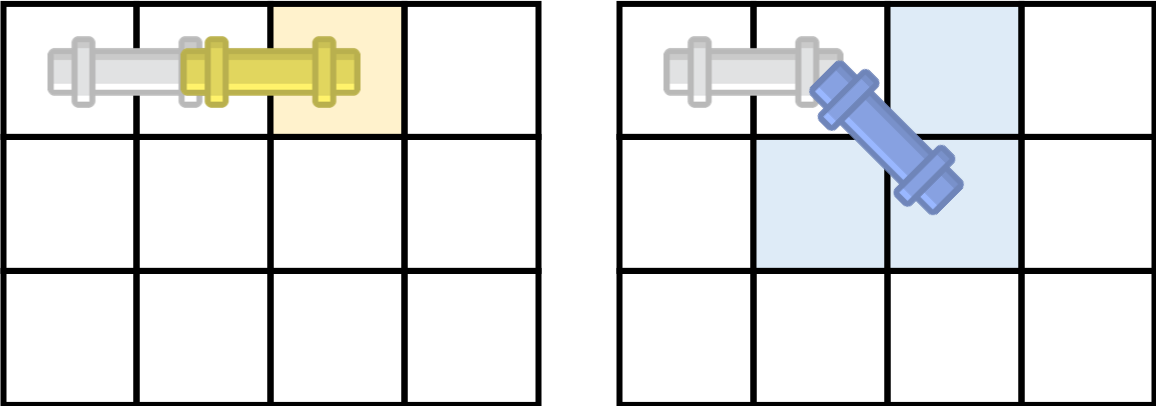
가로

세로

대각선
가장 처음에 파이프는 (1, 1)와 (1, 2)를 차지하고 있고, 방향은 가로이다. 파이프의 한쪽 끝을 (N, N)로 이동시키는 방법의 개수를 구해보자.
입력
첫째 줄에 집의 크기 N(3 ≤ N ≤ 16)이 주어진다. 둘째 줄부터 N개의 줄에는 집의 상태가 주어진다. 빈 칸은 0, 벽은 1로 주어진다. (1, 1)과 (1, 2)는 항상 빈 칸이다.
출력
첫째 줄에 파이프의 한쪽 끝을 (N, N)으로 이동시키는 방법의 수를 출력한다. 이동시킬 수 없는 경우에는 0을 출력한다. 방법의 수는 항상 1,000,000보다 작거나 같다.
제한
예제 입력 1
3
0 0 0
0 0 0
0 0 0예제 출력 1
1예제 입력 2
4
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0예제 출력 2
3
예제 입력 3
5
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0예제 출력 3
0예제 입력 4
6
0 0 0 0 0 0
0 1 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0예제 출력 4
13출처
알고리즘 분류
- DP
- 그래프 이론
- 그래프 탐색
접근 방법
처음 봤을 때는 N의 크기가 크지 않아, 충분히 완전 탐색으로도 풀 수 있는 문제라고 생각하여 구현 하였고, 정답처리를 받았다.
이 후, 각 위치간의 특정 관계가 있음을 파악했고 해당 문제를 DP방식으로도 구현하여 정답 처리를 받았다.
먼저, 문제에서 →, ↘, ↓ 방향으로 움직이는 것만 가능하다고 하였으므로 파이프의 앞과 뒤는 절대 반전되어 나타 날 수가 없다.
|
.................... |
,,,,,,,,,,,,,,,,,,, |
|
,,,,,,,,,,,,,,,,,,, |
................. |
편의 상 파란색을 파이프의 앞면이라고 하였을 때, 절대 위와 같은 형태로 파이프가 존재할 수가 없다는 것이다.
고로, 우리는 위와 같은 상황을 고려할 필요가 없이 파이프의 앞 부분의 좌표가 (N,N)일 때만 고려하면 된다.
완전탐색
탐색을 파이프의 앞면에서 부터 시작한다고 하자, 탐색을 하면서 조심해야 할 점은 파이프의 front와 back에 따라 현재 놓여 있는 파이프의 상태( 대각선으로 놓여 있는지, 가로로 놓여 있는지, 세로로 놓여 있는지 )가 결정되고 이에 따라 다음 탐색 때 가능한 위치의 경우가 바뀐다는 점이다.
한번 움직 일 때 최대 45도 회전을 시킬 수 있으므로, 파이프가 가로로 놓여 있을 때는 가로로 움직이거나 대각선으로 움직일 수가 있고
세로로 놓여 있을 때는 세로로 움직이거나 대각선으로 움직일 수가 있고 대각선 상태에서는 가로, 세로, 대각선 모든 방향으로 움직 일 수가 있다.
먼저 해당 방향으로 움직인 다음, 해당 움직임이 유효한지 체크를 해주는 check() 함수를 조건에 맞추어 구현하였다.
DP
우리가 메모이제이션 할 배열 DP[i][j]를 (i,j)까지 파이프의 앞 부분이 도착할 수 있는 경우의 수
라고 정의를 하자.
그러면 특정 좌표에 도착할 수 있는 경로는 다음과 같이 3개의 방향에서 움직여서 도착하는 경우의 수의 합이 될 것이다.

그런데, 여기서 문제가 하나 있다.
1,2,3번 좌표에 도착하는 모든 경우에서 전부 특정 좌표로 갈 수 있는가? 이다.
그건 아니다.
아래의 그림을 보면, 이와 같은 경우도 위에서 2번 좌표에 도착하는 경우의 수 중 하나라는 것을 알 수 있다.

최대 파이프는 45도만 회전 시킬 수 있으므로, 해당 이동은 불가능하다.
즉, 이전 파이프가 놓여있는 상태에 따라 움직일 수 있는 방향이 제한된다는 것이다.
이전 파이프의 방향까지 고려한 DP table을 다시 정의해보자면 다음과 같다.
DP[i][j][k] = 특정 좌표 (j,k) 까지 i번째 방향(가로, 대각, 세로)으로 파이프를 놓을 수 있는 경우의 수
이렇게 DP table을 정의한다면, 정확한 답을 구할 수 있다.
예를 들자면, 이런식이다.
현재 (ß, µ)에 가로 방향으로 도착할 수 있는 경우의 수 = (ß, µ-1)에 가로 방향으로 도착하는 경우의 수 + (ß-1, µ-1)에 대각 방향으로 도착하는 경우의 수
소스 코드1 ( BFS를 통한 완전 탐색 )
#include <bits/stdc++.h>
using namespace std;
enum{ HORIZONAL = 0, CROSS = 1, VERTICAL = 2 };
struct Pipe{
pair<int,int> fr,bk;
int currentDirType = HORIZONAL;
Pipe(){
fr = {0,1};
bk = {0,0};
}
};
int n;
int board[17][17];
Pipe movePipe(Pipe pip, int direction){
if( direction == HORIZONAL ){
pip.bk = pip.fr;
pip.fr.second += 1;
}
else if( direction == CROSS ){
pip.bk = pip.fr;
pip.fr.first += 1;
pip.fr.second += 1;
}
else{
pip.bk = pip.fr;
pip.fr.first += 1;
}
return pip;
}
bool check(Pipe p, int prev_dir){
// 이전에 옮긴 명령이 정당한가?
if( p.fr.first >= n || p.fr.second >= n || p.fr.first < 0 || p.fr.second < 0)
return false;
switch(prev_dir){
case HORIZONAL:
if( board[p.fr.first][p.fr.second] == 1 ) return false;
break;
case VERTICAL:
if( board[p.fr.first][p.fr.second] == 1 ) return false;
break;
case CROSS:
if( board[p.fr.first][p.fr.second] == 1 ||
board[p.fr.first-1][p.fr.second] == 1 ||
board[p.fr.first][p.fr.second-1] == 1 )
return false;
break;
}
return true;
}
int main(void){
ios_base::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n;
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
cin >> board[i][j];
}
}
Pipe pipe;
queue<Pipe> Q;
Q.push(pipe);
int answer = 0;
while(!Q.empty()){
Pipe E = Q.front(); Q.pop();
if( E.fr.first == n-1 && E.fr.second == n-1 ){
answer += 1;
continue;
}
if( E.currentDirType == HORIZONAL ){
Pipe next1 = movePipe(E, HORIZONAL);
Pipe next2 = movePipe(E, CROSS);
next2.currentDirType = CROSS;
if( check(next1, HORIZONAL) )
Q.push(next1);
if( check(next2, CROSS) )
Q.push(next2);
}
else if( E.currentDirType == VERTICAL ){
Pipe next1 = movePipe(E, VERTICAL);
Pipe next2 = movePipe(E, CROSS);
next2.currentDirType = CROSS;
if( check(next1, VERTICAL) )
Q.push(next1);
if( check(next2, CROSS) )
Q.push(next2);
}
else{
// cross line
Pipe next1 = movePipe(E, HORIZONAL);
next1.currentDirType = HORIZONAL;
Pipe next2 = movePipe(E, VERTICAL);
next2.currentDirType = VERTICAL;
Pipe next3 = movePipe(E, CROSS);
next3.currentDirType = CROSS;
if( check(next1, HORIZONAL) )
Q.push(next1);
if( check(next2, VERTICAL) )
Q.push(next2);
if( check(next3, CROSS) )
Q.push(next3);
}
}
cout << answer ;
return 0;
}
소스 코드2 ( DP 활용 )
#include <bits/stdc++.h>
using namespace std;
enum{ HORIZONAL = 0, VERTICAL = 1, CROSS = 2 };
int board[17][17];
int main(void){
ios_base::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n;
cin >> n;
for(int i=0; i<n; i++){
for(int j=0; j<n; j++)
cin >> board[i][j];
}
// base case
int dp[3][17][17] ={0, };
for(int i=1; i<n; i++){
if( board[0][i] == 1 ) break;
dp[HORIZONAL][0][i] = 1;
}
for(int i=1; i<n; i++){
for(int j=1; j<n; j++){
if( board[i][j] == 1 )
continue;
// 가로로 현재 위치에 도착할 수 있는 경우
dp[HORIZONAL][i][j] = dp[HORIZONAL][i][j-1] + dp[CROSS][i][j-1];
// 세로로 현재 위치에 도착할 수 있는 경우
dp[VERTICAL][i][j] = dp[VERTICAL][i-1][j] + dp[CROSS][i-1][j];
// 대각선 모양으로 현재 위치에 도착할 수 있는 경우
if( board[i-1][j] != 1 && board[i][j-1] != 1 )
dp[CROSS][i][j] = dp[CROSS][i-1][j-1] + dp[HORIZONAL][i-1][j-1] + dp[VERTICAL][i-1][j-1] ;
}
}
int answer = 0;
for(int i=0; i<3; i++)
answer += dp[i][n-1][n-1];
cout << answer;
return 0;
}'자료구조 + 알고리즘 > [BOJ]' 카테고리의 다른 글
| [BOJ] 2580번- 스도쿠 (0) | 2020.12.04 |
|---|---|
| [BOJ] 1946번 - 신입 사원 (0) | 2020.12.02 |
| [BOJ] 1958번 - LCS 3 (0) | 2020.11.28 |
| [BOJ] 14499번 - 주사위 굴리기 (0) | 2020.11.24 |
| [BOJ] 2529번: 부등호 (0) | 2020.11.23 |


